 /
/ 
Time Limit: 4 sec / Memory Limit: 256 MB
配点 : 点
問題文
ぬすけ君は、 のグリッドを持っています。行には上から順に から 、列には左から順に から の番号がついています。 グリッドの各マスは白か青かに塗られており、 が のとき 行 列のマスは青マス、 のとき白マスです。 青く塗られた任意の二つのマス について、 からはじめて、現在いるマスから辺を共有する青いマスに進むことを繰り返して に至るような経路のうち、同じマスを 度以上通らないようなものは、高々 通りです。
ぬすけ君の永遠のライバルである怪盗スヌークは、ぬすけ君に 個の質問をしました。 個目の質問は、 つの整数 からなり、 グリッドの 行目から 行目まで、 列目から 列目までの範囲の長方形領域を切り出したときに、 その範囲の青マスからなる連結成分がいくつあるかを答える質問です。
怪盗スヌークの質問すべてに答えてください。
制約
- は または である
- は問題文中の条件を満たす
入力
入力は以下の形式で標準入力から与えられる。
.. : .. :
出力
質問ごとに、その範囲の青マスからなる連結成分がいくつあるかを出力せよ。
入力例 1Copy
3 4 4 1101 0110 1101 1 1 3 4 1 1 3 1 2 2 3 4 1 2 2 4
出力例 1Copy
3 2 2 2
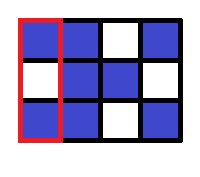
つ目の質問では、グリッド全体が指定されます。青マスからなる連結成分は つあるので、 を出力します。
つめの質問では、赤枠の範囲が指定されます。青マスからなる連結成分は つあるので、 を出力します。 もとのグリッドで同じ成分に属するマスが、異なる成分に属するかもしれないことに注意してください。
入力例 2Copy
5 5 6 11010 01110 10101 11101 01010 1 1 5 5 1 2 4 5 2 3 3 4 3 3 3 3 3 1 3 5 1 1 3 4
出力例 2Copy
3 2 1 1 3 2
Score : points
Problem Statement
Nuske has a grid with rows and columns of squares. The rows are numbered through from top to bottom, and the columns are numbered through from left to right. Each square in the grid is painted in either blue or white. If is , the square at the -th row and -th column is blue; if is , the square is white. For every pair of two blue square and , there is at most one path that starts from , repeatedly proceeds to an adjacent (side by side) blue square and finally reaches , without traversing the same square more than once.
Phantom Thnook, Nuske's eternal rival, gives queries to Nuske. The -th query consists of four integers , , and and asks him the following: when the rectangular region of the grid bounded by (and including) the -th row, -th row, -th column and -th column is cut out, how many connected components consisting of blue squares there are in the region?
Process all the queries.
Constraints
- is either or .
- satisfies the condition explained in the statement.
Input
The input is given from Standard Input in the following format:
.. : .. :
Output
For each query, print the number of the connected components consisting of blue squares in the region.
Sample Input 1Copy
3 4 4 1101 0110 1101 1 1 3 4 1 1 3 1 2 2 3 4 1 2 2 4
Sample Output 1Copy
3 2 2 2

In the first query, the whole grid is specified. There are three components consisting of blue squares, and thus should be printed.
In the second query, the region within the red frame is specified. There are two components consisting of blue squares, and thus should be printed. Note that squares that belong to the same component in the original grid may belong to different components.
Sample Input 2Copy
5 5 6 11010 01110 10101 11101 01010 1 1 5 5 1 2 4 5 2 3 3 4 3 3 3 3 3 1 3 5 1 1 3 4
Sample Output 2Copy
3 2 1 1 3 2